There is an important assumption made by proponents of reservations (and occasionally, this is a point conceded by those who oppose it). It sounds like the following:
The Backward Classes are disadvantaged. Hence they are unable to develop skills (that are required for competing). This is due to lower intelligence due to poor childhood nutrition, an environment that is not conducive to skill development, and other such factors. By enforcing quotas so that lower skill candidates get access to centres of excellence, the next generation is more likely to possess the skills required to compete, and society, as such, will benefit through access to more productive human resources (within multiple, if not within one generation)
Although it appears very plausible first hand, let us analyse the implications in terms of cost to society and productivity. Let us also (in a sense) bring in the notion of comparative advantage amongst groups, in a setting where the education of parents affects the skill sets of children. I will not address the issue of ``social justice", for it is not clear to me what that means. I will make the following assumptions.
1. There are two groups in society - The advantaged/high skilled group (H) and the disadvantaged/low skilled group (L). Time proceeds in discrete steps, each step corresponding to a generation.
2. There are two kinds of educational resources - Good (G) and Bad (B) with a fixed number of seats each.
3. Good educational resources are costlier to society.
4. Each agent, when she dies, produces a child. The child could be advantaged or disadvantaged with probabilities that depend on the kind of agent that she is, and the level of education she received.
5. The probabilities are such that if an agent has received good schooling, whether they were advantaged or not does not matter, they are equally likely to produce an advantaged child, and this likelihood is significantly greater than 1/2. On the other hand, disadvantaged agents that get poor schooling are very unlikely to produce advantaged children. This is the standard argument used in support of reservations.
6. Advantaged agents that are ``forced" to go to a bad school have a lower likelihood of producing an advantaged child than if they had got a good education. These likelihoods are indicators of social mobility, and will have a large role to play in our subsequent analysis.
Ok, so I hope you are with me. Go back to my assumptions and check them. Note down any disagreements. Especially look at number 5. It implies that regardless of what you do, in the ``steady state" there will always be disadvantaged agents in the society (and also, somewhat trivially, that the population is constant, which is not so serious, because I have never heard any arguments in support of reservations that appeal to population growth).
Now, coming to the productivity of the agents.
7. Before dying, agents produce an amount of goods that is defined by their productivity, and is more than the cost incurred for their education. The productivity of disdvantaged agents is lower than that of the advantaged agents (owing to lower skill-sets). The difference does not matter, it can be arbitrarily small. All that matters is that there is a difference. In my setting I use the following assumption: Productivity (H,G) > Productivity(L, G) > Productivity(H,B) > Productivity(L,B).
8. The total number of seats is the same as the number of agents. This is not such a serious assumption, because in the sense of our stylized setting, ``no education" can be defined as a very weak form of educational resource (with zero cost).
9. ``Good" seats are always scarce resources even for the advantaged group and even in the absence of reservations, in the sense that the number of good seats is less than the number of advantaged agents. Another very crucial assumption that is often ignored by those who advocate reservations.
10. The person who allocates seats to groups is a social planner who is looking to maximise the overall gain to society (production - cost of education). This is the same as the "society as a whole will gain" argument made by those who advocate reservations. The social planner also gives greater weight to gains in the near future than to those in the far future. (Discount factor less than 1)
Right then, so now let us look at what our social planner does. It is easy enough to analyze the ``steady state" that society reaches with these probabilities, with these
assumptions. Solving our little model mathematically , we can establish the following little factoid: For each constant reservation policy (defined as the proportion of good seats allocated to disadvantaged agents), there is a unique steady state. For a given value of parameters, the utility of the planner is monotonic (either increasing or decreasing) in the reservation policy.
That is, depending on the value of costs/productivities/progeny assumed, the ``best" reservation policy is either 100% or 0, but nowhere in between.
I am not going to go into the model, but i will intuitively explain it. What constrains the level of skill in society is the number of good seats. As long as good seats are scarce resources, society is always better of giving off all the good seats to the greater productivity agents. However, for some values of the probability of producing productive offspring and their relative productivities, it is always better for society to allocate all the good seats to the disadvantaged agents. The policy takes an "all or nothing" form depending the values of parameters.
What the model is very sensitive to is this: If the progeny of an advantaged agent who was forced to get a poor education still has a decent likelihood of being advantaged, and at the same time the progeny of a disadvantaged agent who was forced to get a poor education is very unlikely to be advantaged, then a policy of 100% reservations works.
If the difference between these likelihoods is not as stark, then a policy of no reservations at all is the best policy.I will show you some pictures now. I have fixed the values of other parameters, and considered a population of 100 with 20 good seats available. The first picture is the effect the social mobility for poorly educated people has on the optimal reservation policy. The knife edge is clearly visible. The second is the gain to society depending on the mobility. It shows that society gains with greater social mobility. The third is the number of advantaged people in the society.
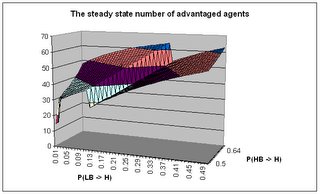You will see a cliff in this picture, and it corresponds to the knife edge where it suddenly become more optimal to have no reservations at all, and suffer a lack of advantaged workers.The interesting point to be noted around this cliff that for the same level of utility to the planner, reservations increase the number of advantaged workers in society. I am unwilling, however, to attach any social justice implications to this. Have fun with these pictures. With such a simplistic model, it is amazing the level of complexity you can get. And I have not even talked about relative productivity effects!!
This is admittedly a rather shallow analysis, and I am sure alternate settings could be imagined, which could, perhaps lead to completely different conclusions. But it is very interesting indeed.
(This work is preliminary and incomplete and may not be cited.)
2 comments:
Nice. Though you realise that we're dealing with people who can't handle basic reasoning here, so three dimensional graphs are a bit much.
Also, as I understand it, you're assuming that productivity of each class of actors is independent of their proportion in the population. That's not necessarily true - though it's probably more an interesting next step than a necessity for this model.
MR: Good point, but I don't think we need to muddy it with all this personal discomfort stuff. The simpler point is that if there's a distribution of productivity and an individual's productivity levels can be measured at every stage, then the planner should just set a global productivity cut-off on the overall distribution and let that map back to the distributions among the different categories. He doesn't even need to think about the profile of the population.
heh heh: One other thought. It feels like you're assuming that utility levels map directly to productivity. But if you assume that marginal utility of income is declining then disadvantaged actors would have higher utility from equivalent or lower levels of income. If that's true, then it's a question of whether the planner's trying to maximise overall production or overall utility. It may be possible (depending on the relative size of the difference in marginal utility and productivity between advantaged and disadvantaged categories) to actually raise welfare while cutting down on production. You could argue that that's unfair to the advantaged player because his utility is going down, but it's still likely to be higher than that of the disadvantaged player in absolute terms, and there's no a priori reason why a social planner should be trying to maximise production over utility.
to illustrate: imagine that advantaged actors earn incomes of 100 or 120 depending on whether they go to good schools or not. Imagine that the comparable numbers for disadvantaged actors are 50 and 65. But that the (constant) marginal utility of an extra income unit is 1 utility unit for the advantaged and 1.5 utility units for the disadvantaged. In that case, shifting the school allocation from the advantaged to the disadvantaged would lower income levels overall by 5 units, but raise utility levels by 2.5 units.
Post a Comment